My model is roughly like this: one material encloses another in the shape of a hemisphere. However, I encountered errors when meshing the hemisphere within the mesh.
Since you’re a beginner, I might recommend you watch this webinar we recorded and put on YouTube that talks about the fundamental strategy for hex-meshing in Cubit. In particular, you might pay close attention to the discussion at 4:30 - 13:00 that talks about how the overall strategy.
Here’s a journal file that I believe reproduces your geometry:
reset
sphere r 1
bri x 8
undo group begin
webcut volume all with plane xplane offset 0
delete volume 3, 4
subtract volume 1 from volume 2 keep_tool
compress ids
What I like to do at this point is make any of my simulation “set” assignments. Cubit is based on the open-source Exodus mesh format developed by Sandia National Labs which uses block for element regions, sideset for boundaries, nodeset for nodes. I make these assignments now since afterwards I’m going to start partitioning the geometry for meshing, and these assignments will be “inherited” by the entities produced by partitioning – this simplifies set assingment.
block 1 vol 1
block 2 vol 2
block 1 name "inclusion"
block 2 name "matrix"
sideset 1 surface 2 9
sideset 1 name "xmin"
My next step is I think about the different mesh schemes that are available in Cubit, and whether they’re applicable. Something that stands out to me is that I know the polyhedron scheme is really good for meshing cubes with a “blunted” corner:
And I can “see” how, if I cut the yellow volume into quarters:
webcut volume all with plane yplane
webcut volume all with plane zplane
that I’ll end up with volumes that will have the same topology as the “blunted cube” and thus, could be meshed with the polyhedron scheme:
vol in block 2 scheme polyhedron
I can also see how cutting the sphere into quarters will result in shapes that are topological tetrahedra – and Cubit has a meshing scheme called TetPrimitive that meshes topological tetrahedra.
vol in block 1 scheme tetprimitive
Putting all these together, then, and including the mesh command as well as the merge command to enforce a contiguous mesh between the separate volumes. Note, however, that whenever tetprimitive works, so too will the polyhedron scheme – however the polyhedron scheme has requirements that all of the volume’s surfaces are also set to polyhedron… if you apply the tetprimitive scheme after the polyhedron scheme it will overwrite the polyhedron setting and Cubit won’t be able to generate the mesh. The solution is to either apply polyhedron schemes last or to apply polyhedron scheme to the tetprimitive volumes. I’ve chosen the first of these options below:
## Create the geometry
reset
sphere r 1
bri x 8
undo group begin
webcut volume all with plane xplane offset 0
delete volume 3, 4
subtract volume 1 from volume 2 keep_tool
compress ids
## Make set assignments
block 1 vol 1
block 2 vol 2
block 1 name "inclusion"
block 2 name "matrix"
sideset 1 surface 2 9
sideset 1 name "xmin"
## Partition the geometry for meshability
webcut volume all with plane yplane
webcut volume all with plane zplane
## Enforce contiguous mesh (generally need to imprint, not necessary here)
merge all
## Assign mesh schemes
vol in block 1 scheme tetprimitive
vol in block 2 scheme polyhedron
## Generate the mesh
mesh vol all
The resulting mesh, colored by volume ids:
The resulting mesh colored by block ids (draw block all):
Thank you for your advice, I am learning. Additionally, if my material parameters vary smoothly, how should I assign values to the material parameters? For example, the material parameters of block 2 vary as shown in this figure.
That will depend a bit on the solver that you’re using. The solvers that I’ve used that support spatially varying material properties tend to have material models that support spatially-varying properties, where the spatial distribution is defined by a built-in spatial function or a user-provided subroutine, or by an Exodus variable containing the values. The Exodus variable would be assigned to the Exodus mesh after export, using one of the SEACAS library’s tools, such as mat2exo, txtexo, or exodus.py.
For the mat2exo and txtexo tools, you’ll need to build the SEACAS library, but starting with Coreform Cubit 2024.3 we now package exodus.py with Coreform Cubit (on Windows, you can find it at C:\Program Files\Coreform Cubit 2024.3\bin\exodus.py). Here is an example of using exodus.py to create a (nodal) variable and assign it to an Exodus mesh file.
I encountered another issue: the top surface and the weld interface of the model are obtained by ‘webcut’ from a surface represented by a discrete set of points (with analytical formulas). After cutting the model as you suggest above, specifying the format of the middle block as “polyhedron” resulted in an error: “Volume 2 can’t use scheme polyhedron because Vertex 10 has 2 curves in the volume; it must have 3. ERROR: Volume 3 is incompatible with scheme polyhedron…”
I also attempted to use the “map” and “submap” formats, but encountered errors as well.
Here is my script
import cubit
try:
cubit.init(['cubit','-nojournal'])
except:
pass
elementsize1 = 80
elementsize2 = 80
elementsize3 = 80
cubit.cmd('reset')
cubit.cmd('sphere radius 1200.0')
cubit.cmd('volume 1 move x 2995 y 2995.0')
cubit.cmd('webcut vol 1 with zplane')
cubit.cmd('delete vol 1')
#volume 3
cubit.cmd('vol 2 copy')
cubit.cmd('brick x 7000 y 7000 z 5000')
cubit.cmd('volume 4 move x 3500 y 3500 z -2500') # origin 0, 0, 0 [0, -5000]
cubit.cmd('volume 4 move x -500 y -500') # [-500 6500]
cubit.cmd('subtract vol 3 from vol 4')
cubit.cmd('undo group begin')
cubit.cmd('compress')
cubit.cmd('import "topo_coarse.cub" ')
cubit.cmd('import "layer3_coarse.cub" ')
cubit.cmd('webcut vol 1 2 tool body 3')
cubit.cmd('delete vol 5 6')
cubit.cmd('delete body 3')
cubit.cmd('webcut vol 2 tool body 4')
cubit.cmd('delete body 4')
cubit.cmd('compress')
cubit.cmd('sideset 1 surface 2 4')
# avoids assigning empty blocks
cubit.cmd('set duplicate block elements on')
cubit.cmd('merge all')
cubit.cmd('imprint all')
#make set assignments
cubit.cmd('block 1 vol 1')
cubit.cmd('block 2 vol 3')
cubit.cmd('block 3 vol 2')
cubit.cmd('webcut volume in block 1 2 with plane xplane offset 2995')
cubit.cmd('webcut volume in block 1 2 with plane yplane offset 2995')
cubit.cmd('webcut volume in block 2 with plane zplane offset -1800')
# Assign mesh schemes
cubit.cmd('vol in block 1 scheme tetprimitive')
cubit.cmd('vol in block 2 scheme polyhedron')
cubit.cmd('vol in block 3 scheme polyhedron')
#mesh the volumes
cubit.cmd('vol in block 1 size '+str(elementsize1))
cubit.cmd('vol in block 2 size '+str(elementsize2))
cubit.cmd('vol in block 3 size '+str(elementsize3))
cubit.cmd('mesh vol all')
topo_coarse.cub (2.4 MB)
layer3_coarse.cub (551.7 KB)
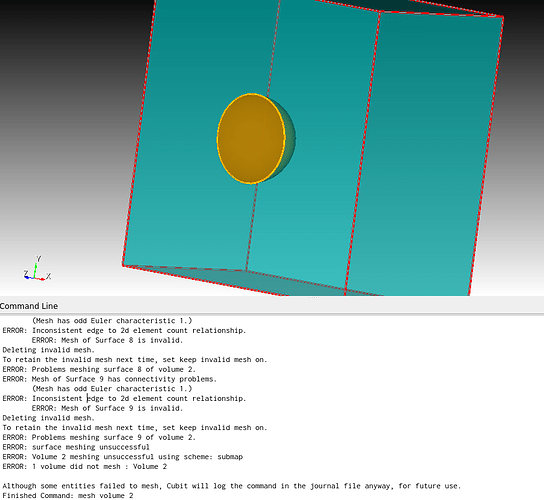
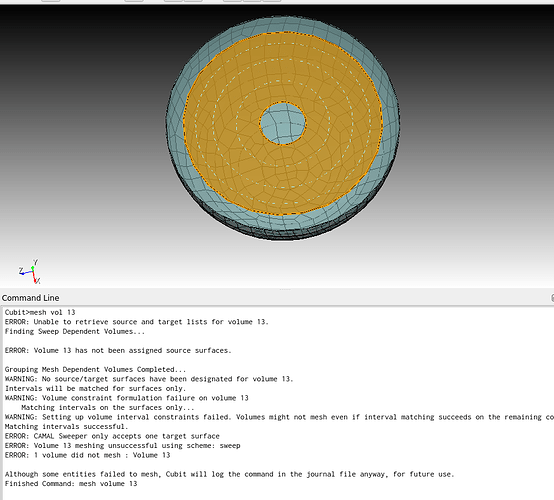
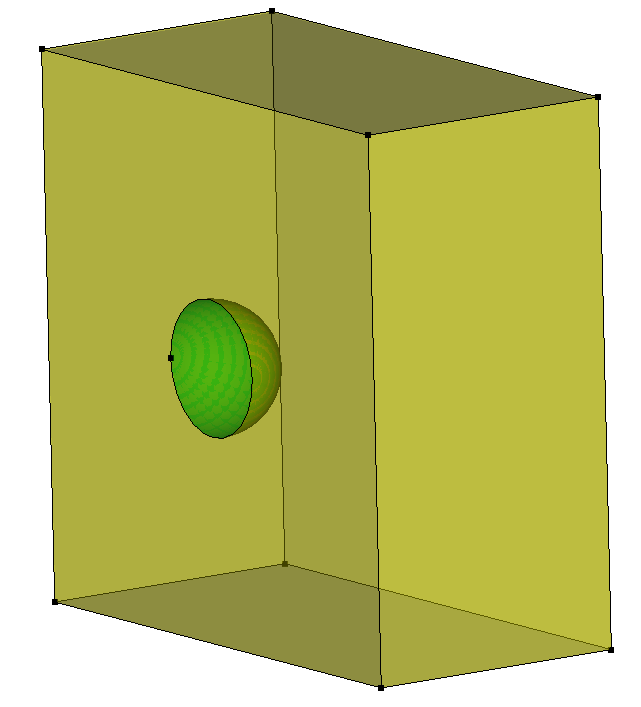
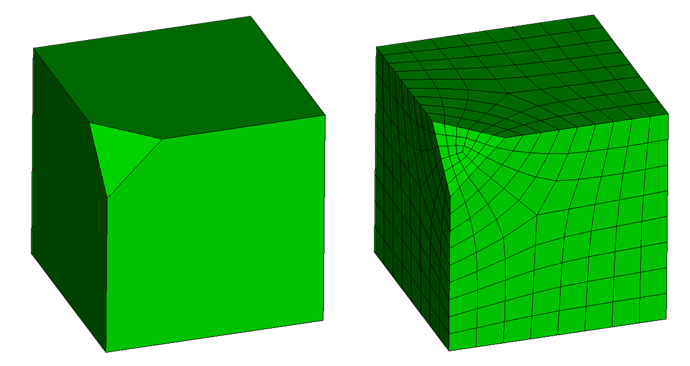
You’re very close… a few comments:
cubit.cmd('merge all')
cubit.cmd('imprint all')
99.9% of the time, you want to imprint all first, and then merge all second
cubit.cmd('merge all')
cubit.cmd('imprint all')
#make set assignments
cubit.cmd('block 1 vol 1')
cubit.cmd('block 2 vol 3')
cubit.cmd('block 3 vol 2')
cubit.cmd('webcut volume in block 1 2 with plane xplane offset 2995')
cubit.cmd('webcut volume in block 1 2 with plane yplane offset 2995')
cubit.cmd('webcut volume in block 2 with plane zplane offset -1800')
The point of imprint and merge in this context is to connect/reconnect disconnected volumes to enable a contiguous mesh. Doing imprint/merge and then webcutting (partitioning) defeats the purpose.
So you’ll want to reorganize to this:
# Make set assignments
cubit.cmd('block 1 vol 1')
cubit.cmd('block 2 vol 3')
cubit.cmd('block 3 vol 2')
# Partition for meshability
cubit.cmd('webcut volume in block 1 2 with plane xplane offset 2995')
cubit.cmd('webcut volume in block 1 2 with plane yplane offset 2995')
cubit.cmd('webcut volume in block 2 with plane zplane offset -1800')
# Ensure contiguous mesh
cubit.cmd('imprint all')
cubit.cmd('merge all')
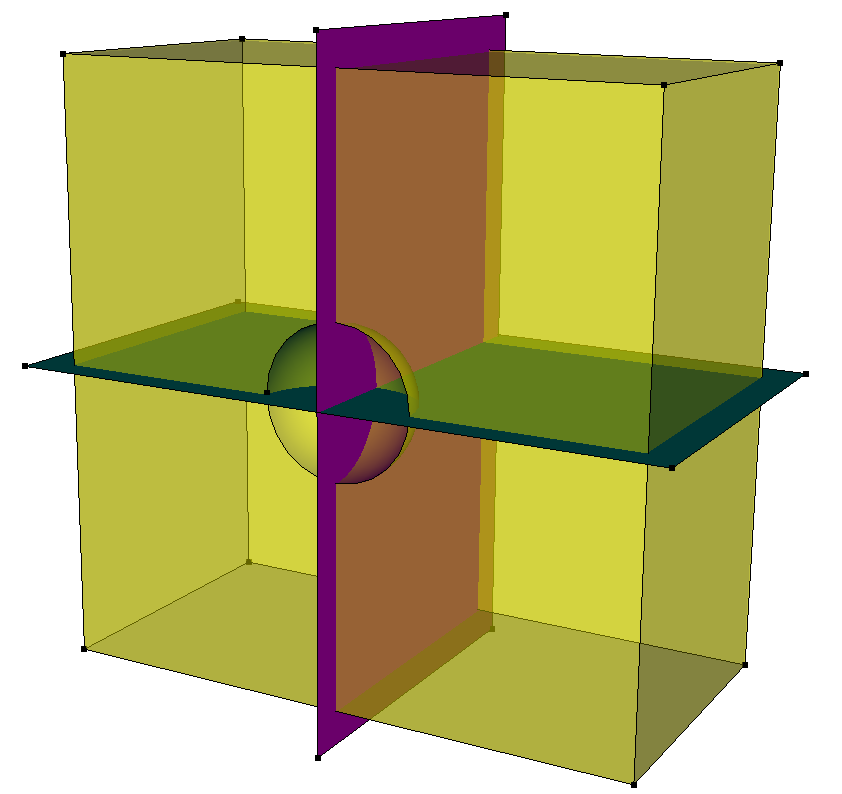
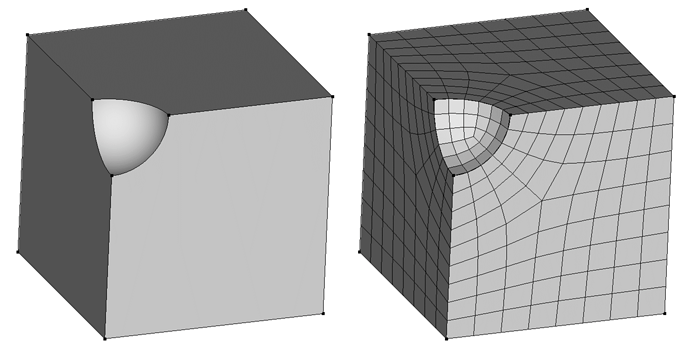
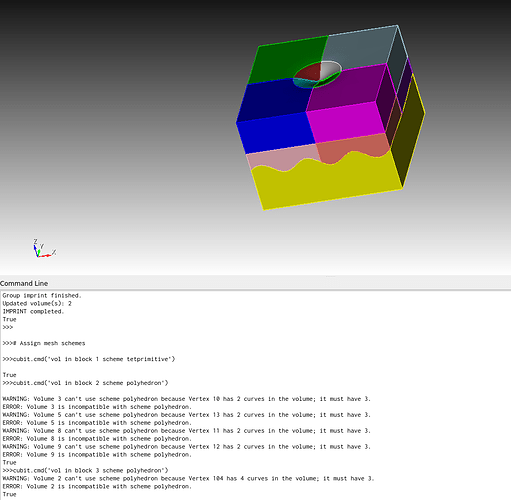
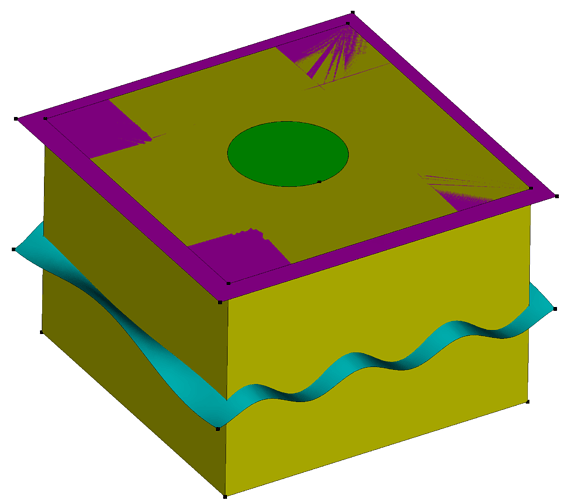
Looking at the geometry immediately before the imprint all command, I find it helpful to visualize vertices with vertex vis on. Essentially, your earlier webcut of the green and yellow volumes with the magenta surface:
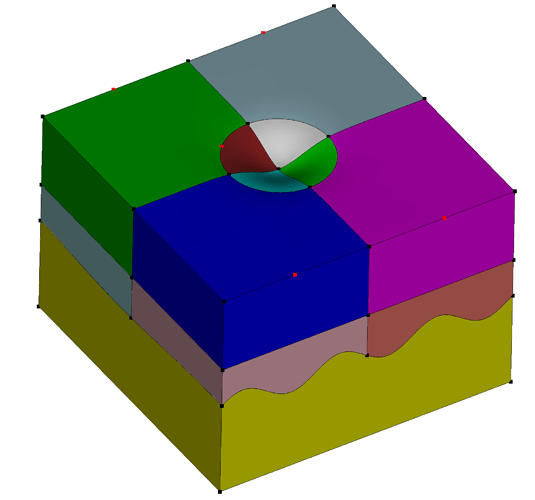
Results in some modification to some of the bounding curves – visualized here as red vertices:
Those vertices are indicators that those curves are “split” – meaning that the topology of the volume has changed and may not be recognizable to Cubit as meshable with the polyhedron scheme. However, assuming that it’s not otherwise critical to the simulation that we exactly maintain the topology (e.g., you’re not applying a boundary condition only to one half of the now-split curve) we can tell Cubit to ignore those vertices in the topology of those volumes, treating the two split curves as a single composite curve:
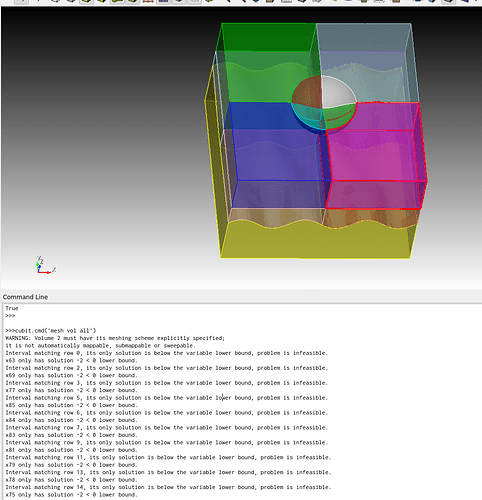
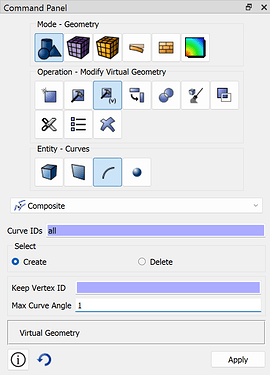
cubit.cmd('composite create curve all angle 1')
Note that we want to do this before we imprint so that the topology won’t be accidentally “frozen” into merged entities:
cubit.cmd('composite create curve all angle 1')
cubit.cmd('imprint all')
cubit.cmd('merge all')
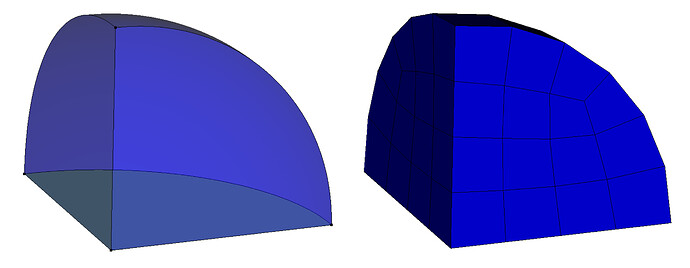
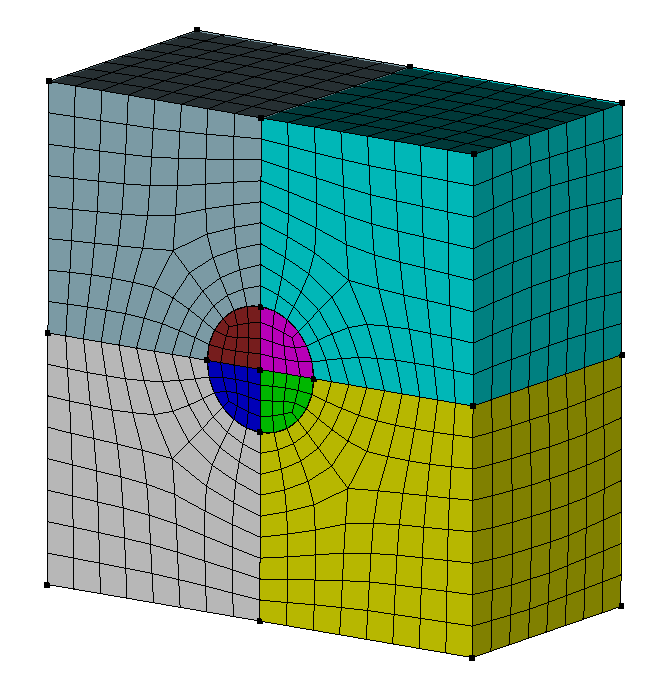
I also reorganized your meshing a bit:
# Assign mesh schemes
cubit.cmd('volume all scheme auto')
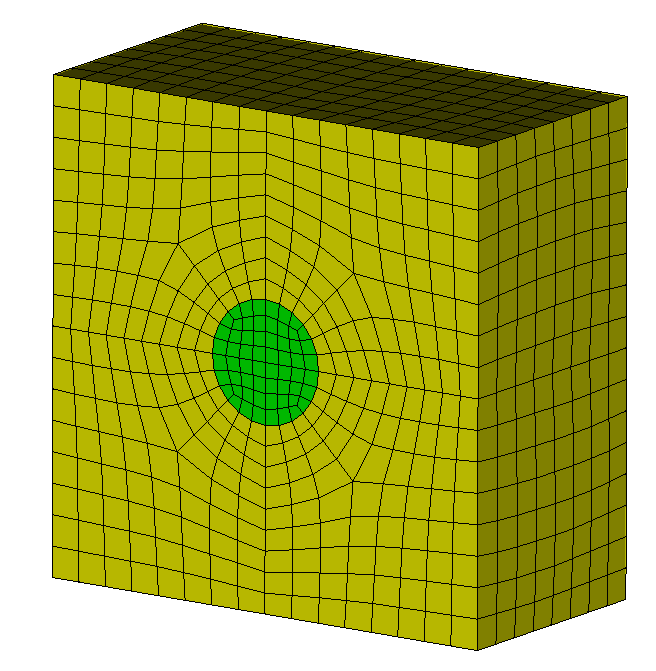
cubit.cmd('vol in block 1 scheme tetprimitive')
cubit.cmd('vol 3 5 8 9 scheme polyhedron')
# Assign mesh sizes
cubit.cmd('vol in block 1 size '+str(elementsize1))
cubit.cmd('vol in block 2 size '+str(elementsize2))
cubit.cmd('vol in block 3 size '+str(elementsize3))
# Mesh volumes
cubit.cmd('mesh vol all with has_scheme "polyhedron"')
cubit.cmd('mesh vol all with has_scheme "tetprimitive"')
cubit.cmd('mesh vol all except with is_meshed')
You might find this documentation page useful to understand the with has_scheme "polyhedron" and except with is_meshed commands:
So the final combined script is:
#!python
elementsize1 = 80
elementsize2 = 80
elementsize3 = 80
cubit.cmd('reset')
cubit.cmd('sphere radius 1200.0')
cubit.cmd('volume 1 move x 2995 y 2995.0')
cubit.cmd('webcut vol 1 with zplane')
cubit.cmd('delete vol 1')
#volume 3
cubit.cmd('vol 2 copy')
cubit.cmd('brick x 7000 y 7000 z 5000')
cubit.cmd('volume 4 move x 3500 y 3500 z -2500') # origin 0, 0, 0 [0, -5000]
cubit.cmd('volume 4 move x -500 y -500') # [-500 6500]
cubit.cmd('subtract vol 3 from vol 4')
cubit.cmd('undo group begin')
cubit.cmd('compress')
cubit.cmd('import "topo_coarse.cub" ')
cubit.cmd('import "layer3_coarse.cub" ')
cubit.cmd('webcut vol 1 2 tool body 3')
cubit.cmd('delete vol 5 6')
cubit.cmd('delete body 3')
cubit.cmd('webcut vol 2 tool body 4')
cubit.cmd('delete body 4')
cubit.cmd('compress')
cubit.cmd('sideset 1 surface 2 4')
# avoids assigning empty blocks
cubit.cmd('set duplicate block elements on')
# Make set assignments
cubit.cmd('block 1 vol 1')
cubit.cmd('block 2 vol 3')
cubit.cmd('block 3 vol 2')
# Partition for meshability
cubit.cmd('webcut volume in block 1 2 with plane xplane offset 2995')
cubit.cmd('webcut volume in block 1 2 with plane yplane offset 2995')
cubit.cmd('webcut volume in block 2 with plane zplane offset -1800')
# Virtual geometry cleanup
cubit.cmd('composite create curve all angle 1')
# Ensure contiguous mesh
cubit.cmd('imprint all')
cubit.cmd('merge all')
# Assign mesh schemes
cubit.cmd( 'volume all scheme auto' )
cubit.cmd('vol in block 1 scheme tetprimitive')
cubit.cmd('vol 3 5 8 9 scheme polyhedron')
# Assign mesh sizes
cubit.cmd('vol in block 1 size '+str(elementsize1))
cubit.cmd('vol in block 2 size '+str(elementsize2))
cubit.cmd('vol in block 3 size '+str(elementsize3))
# Mesh the volumes
cubit.cmd('mesh vol all with has_scheme "polyhedron"')
cubit.cmd('mesh vol all with has_scheme "tetprimitive"')
cubit.cmd('mesh vol all except with is_meshed')
# View the mesh
cubit.cmd( "draw block all" )
