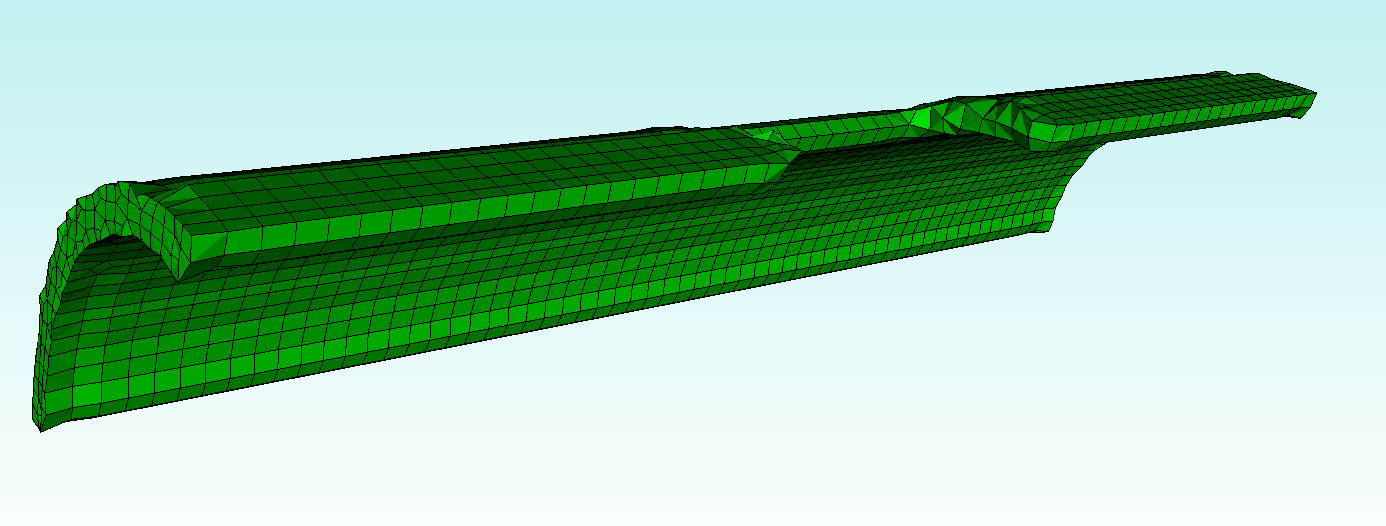
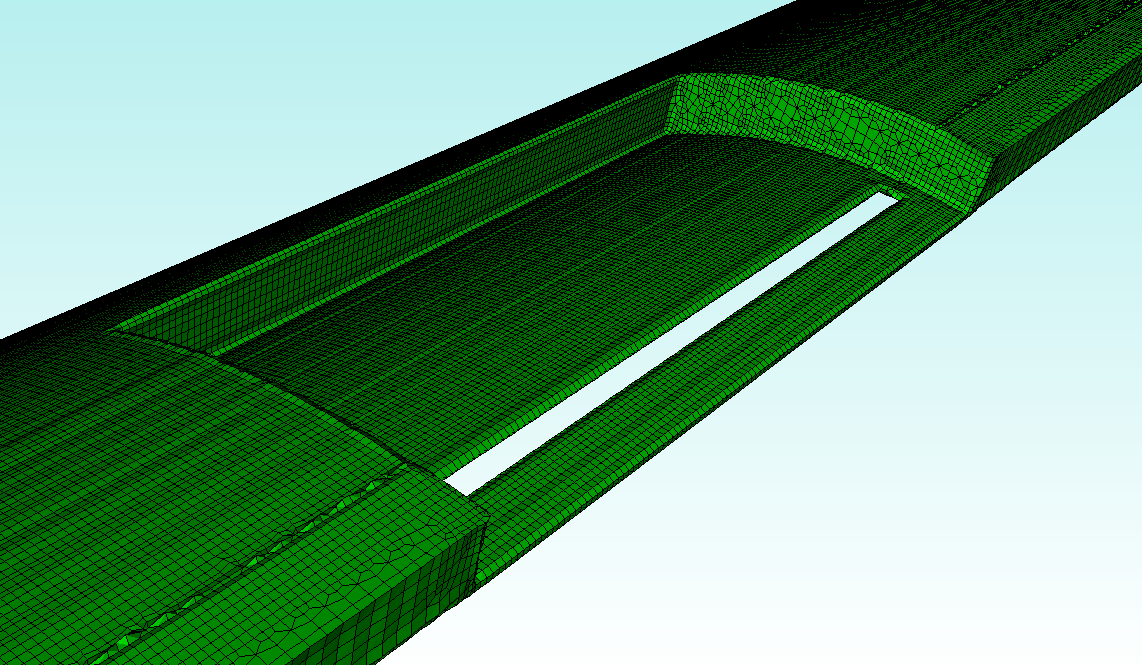
This is a question we get quite often; I thought I’d provide some insight into Sculpt and the general hex-meshing problem that it attempts to solve.
Challenge: Decompose a general volume into quality hexahedral elements
This is an unsolved problem in geometry. There are a number of great texts discussing this challenge and different approaches to hex-meshing. Here are a couple of my favorites:
- Blacker, T. Automated Conformal Hexahedral Meshing Constraints, Challenges and Opportunities. EWC 17, 201–210 (2001). https://doi.org/10.1007/PL00013384
- Owen SJ. 1998. A survey of unstructured mesh generation
technology. Proceedings of the 7th international meshing
roundtable, pp 239–267 (Link)
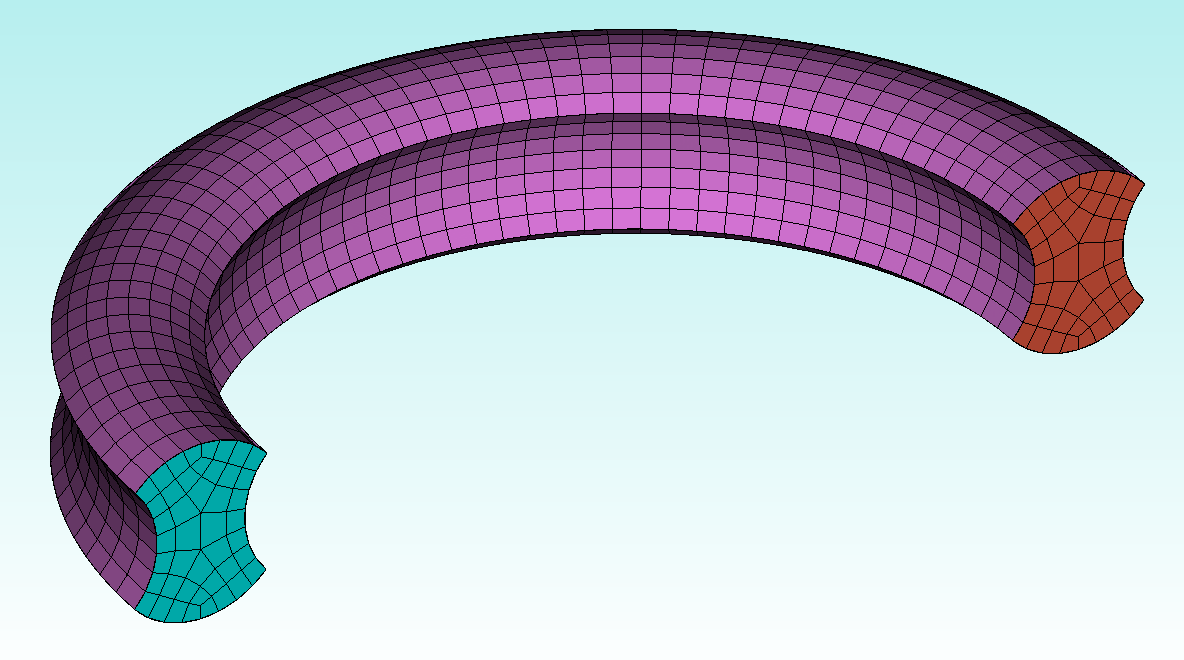
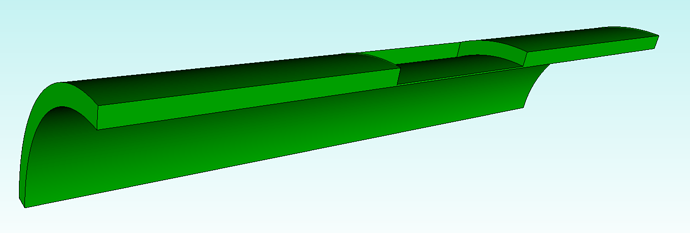
To summarize, it is not yet known how to construct quality hex meshes starting from an arbitrary boundary quad-mesh. For example, for the below geometry we can easily construct a quality surface quadrilateral mesh:
but we don’t know if/how we can create a quality hex-mesh from this layout, whereas with a triangular surface mesh we do know that we can create a quality tetrahedral mesh:
Thus the traditional hex-meshing process requires the user to decompose a part into regions for which we have developed algorithms that do know how to convert a boundary quad-mesh into a volumetric hex mesh. For instance, we can define a mesh on a surface and sweep it along a path to a target surface (which effectively defines the mesh on the “connecting surfaces” and the target surface):
Blue: source – Red: target – Violet: connecting
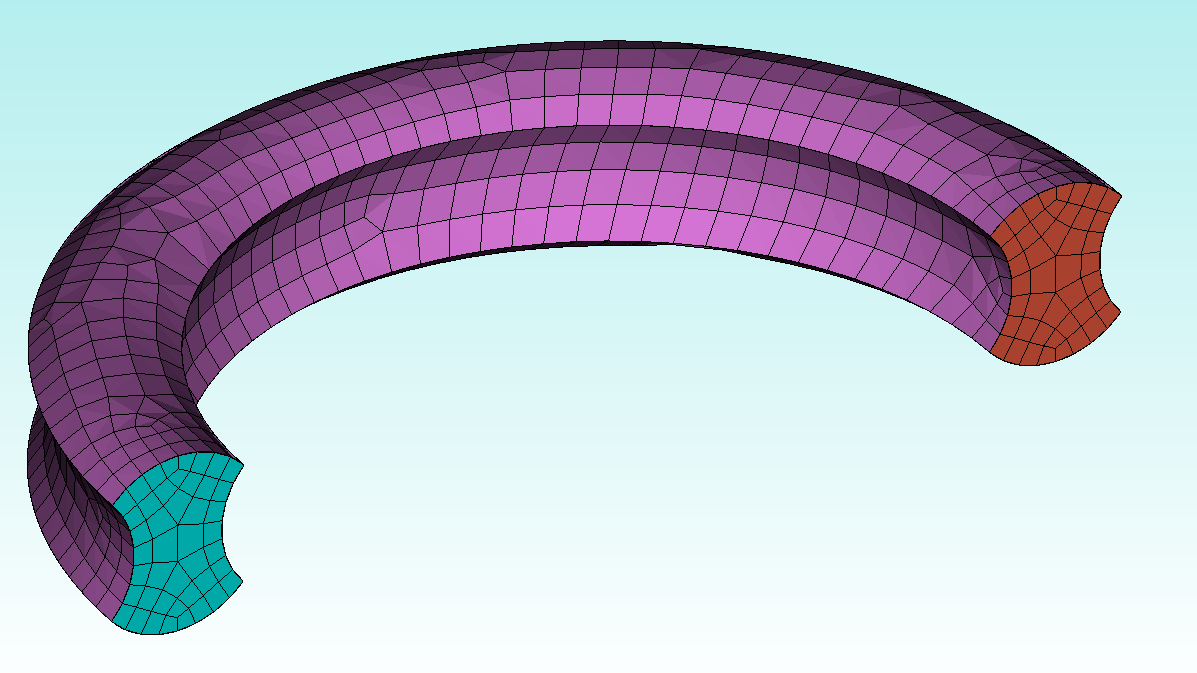
While sweeping is an unstructured mesh, it does have some structure – it is structured along the sweep path. Conversely, if we were to build it fully unstructured, it would suddenly become less clear how to build a hex-mesh:
Even looking at Cubit’s other “unstructured” meshing algorithms, we see that they are really just “blue-print constructions of structured regions”:
-
Sphere
-
Polyhedron
- etc.
So what does Sculpt do?
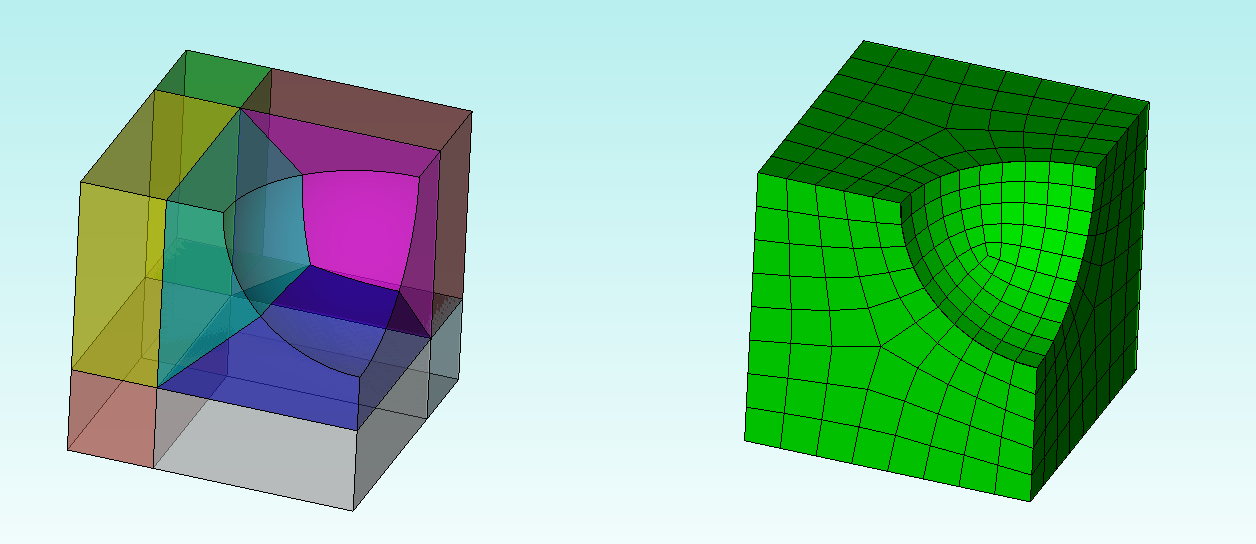
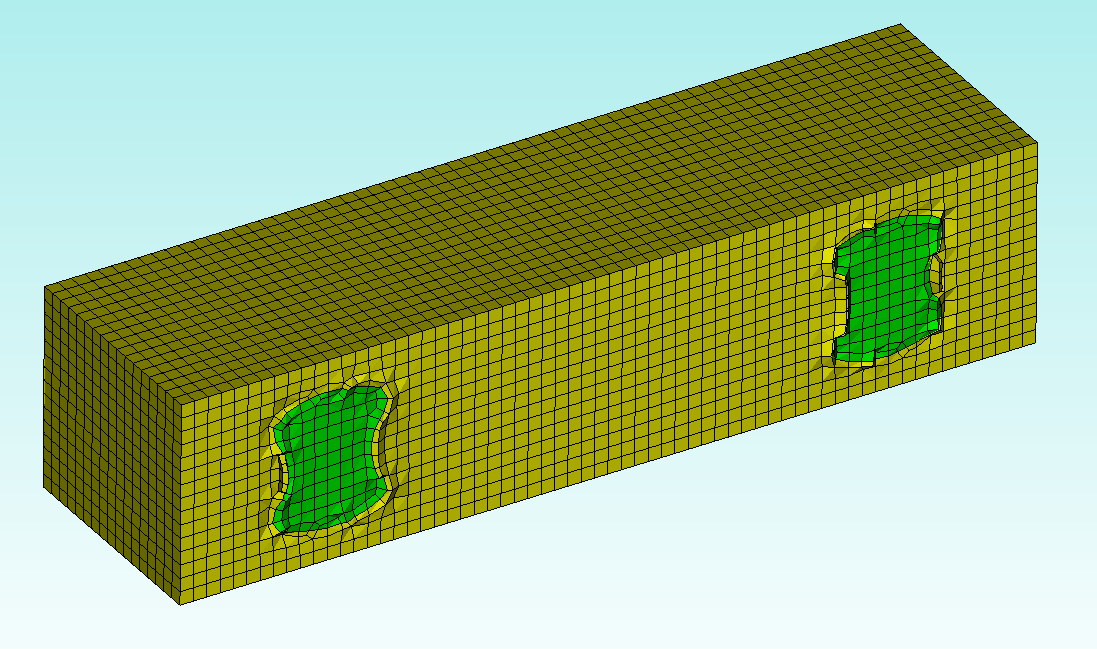
Sculpt takes an entirely different approach. It starts by building a “voxel” mesh of the geometry’s bounding box and identifies each voxel as an interior, boundary, or exterior element:
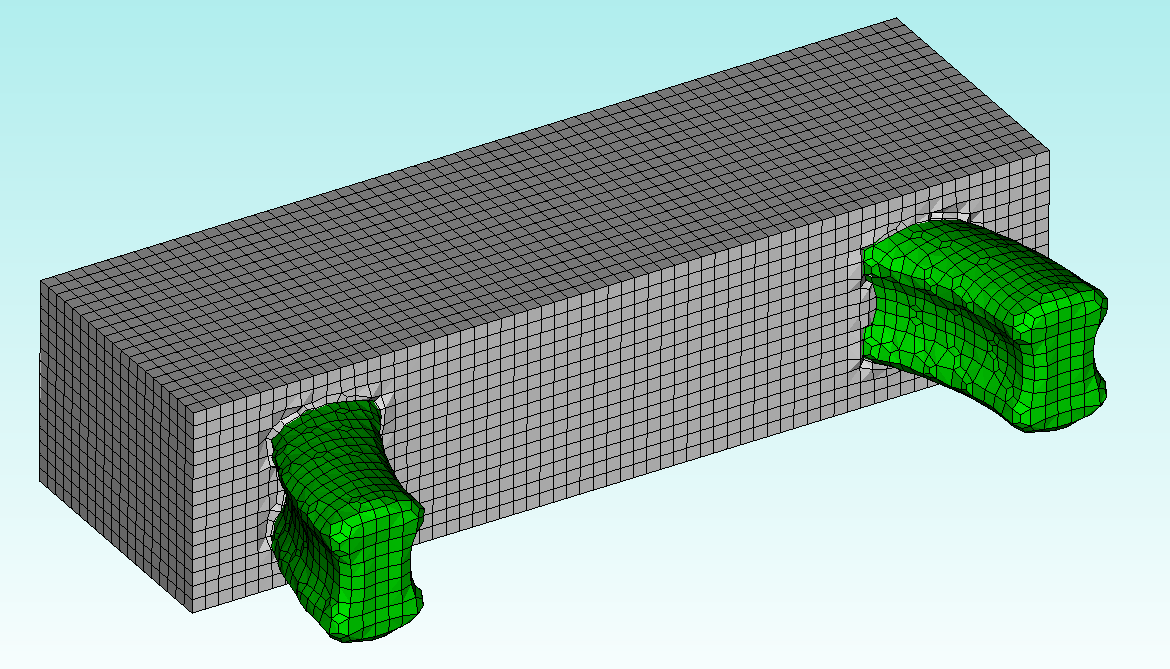
and then “sculpts” the nodes of the hexes on/near the volumes’ boundaries to conform to the geometry. By default, sharp edges are not captured exactly, but are “smoothed over”. Notice that in the images below, the interior elements have near-perfect quality, but the boundary elements tend to be more-poorly shaped and the surface parameterization is not as “beautiful” as when we manually constructed meshes via decomposition:
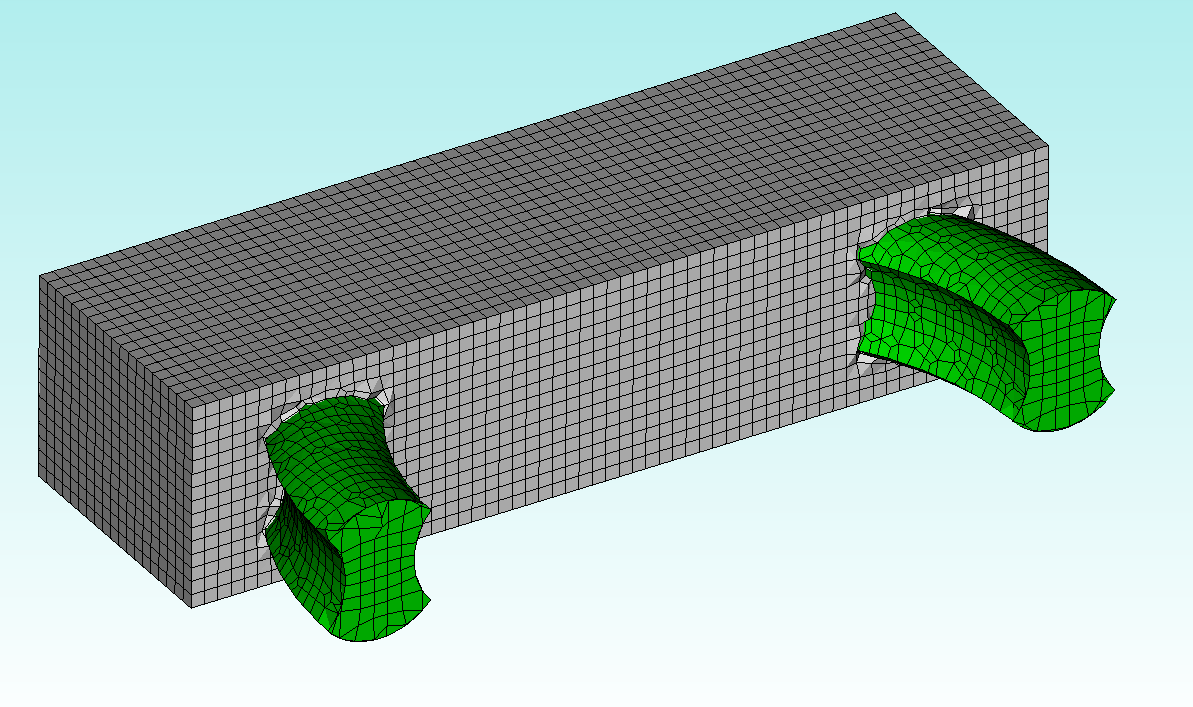
If we switch to running Sculpt as a command-line executable we can pass additional arguments that allow us to capture sharp edges. However, my experience has shown me that it is often quite difficult to build a valid hex-mesh with Sculpt + capture:
It is also possible to add adaptivity which can get a closer approximation to sharp surfaces, without the capture option:
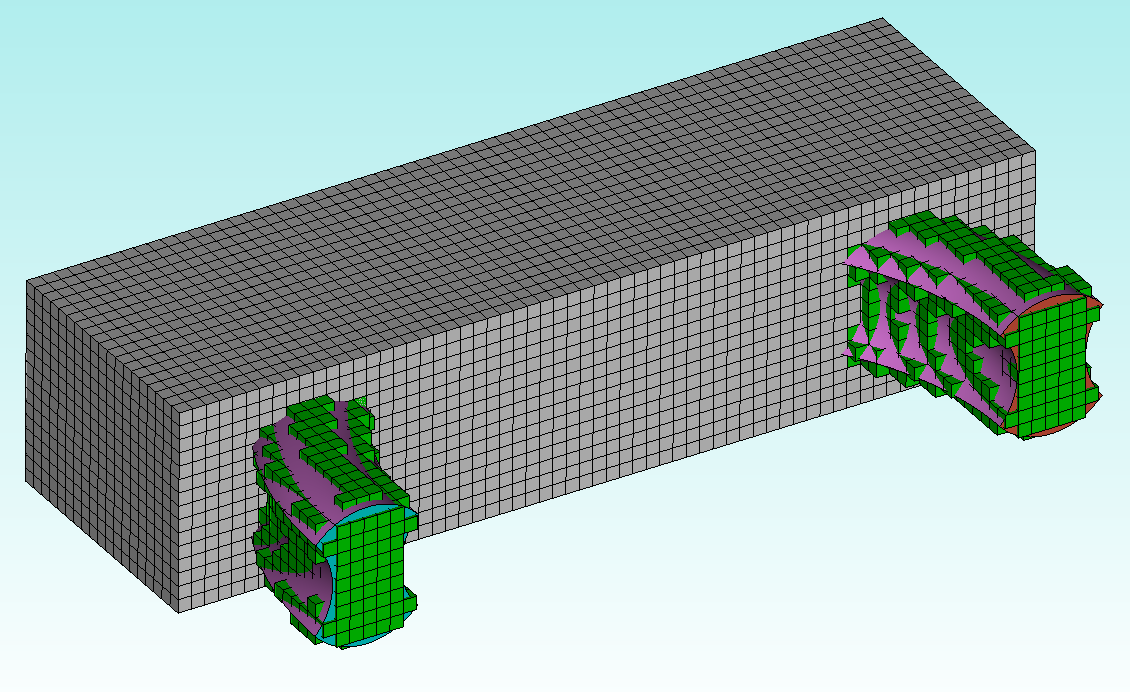
Additionally, Sculpt doesn’t guarantee that all your geometry will be captured. This is especially the case when you have very small features or thin regions in relation to the initial voxel size:
With 3 levels of adaptivity:
When to use Sculpt?
To summarize the two primary hex-meshing techniques in Cubit: 1) Manual partitioning (webcuts) and 2) Sculpt
| Manual | Sculpt |
|---|---|
| Good surface parameterizations | Poor surface parameterizations |
| Element orientation “follows” surfaces | One global element orientation |
| Captures all geometry | Small features may not be captured |
| Decent interior parameterizations | Great interior parameterizations |
| Rarely results in invalid mesh (inverted elements) | Often results in invalid mesh, requiring iterating |
| Can be difficult to get any hex mesh, can require extensive effort to partition | Easy to get a mesh, can be difficult to get a quality mesh. Effort is spent iterating on Sculpt input parameters |
Thus Sculpt is most successful on “blocky” structures (or at least structures where every feature that “matters” is approximately the same size), when exact capturing of the surface isn’t important, and when the quality of the surface mesh isn’t critical to the simulation’s success. Examples of good applications include bones, microstructures, tumors, CT scans of blocky models, etc.
Summary
There are no “silver-bullet” solutions when it comes to hex-meshing. There are times and places to use each of Cubit’s meshing algorithms, whether tetrahedral or hexahedral, partitioning or Sculpting, converting tets to hexes (topic for another post) or using tet/pyramid/hex mixed meshes. These decisions are driven by your project’s technical requirements and business requirements. You may need to use an assortment of multiple approaches to solve your problem. Since there is no single silver-bullet, we’re committed to providing as many kinds of “bullets” in Cubit to aid you in your meshing tasks.