Hi, I’m interested in U-Spline technology and would like to understand how it compares to Hierarchical B-splines and THB-splines in terms of refinement strategy, number of quadrature points per element, and other relevant aspects
Hi @saicctb,
I haven’t worked extensively with Hierachical B-splines or THB-splines, but I did help develop U-splines, so I’ll answer your question the best I can.
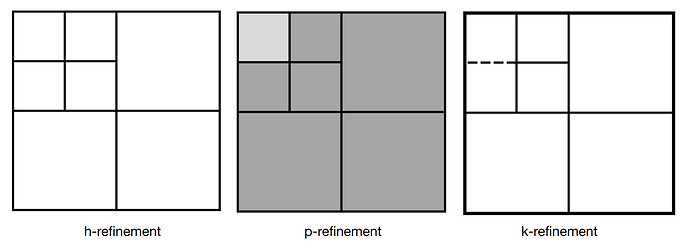
Refinement Strategy
U-splines allow for local h (size), p (degree), and k (continuity) refinement. This is achieved by starting with a linear mesh, and specifying desired degrees on each element and continuity on in interface. Note that this mesh may have T-junctions.
There are certain constraints placed on this refinement, specifically the layout of continuity transitions. We have methods in our software to automatically update the mesh so that those requirements are satisfied. Once this mesh is generated, the U-spline algorithm creates a set of basis functions that are positive, locally linearly independent, and satisfy partition of unity. These basis functions are defined in terms of Bezier extraction. There is a Bezier extraction operator over each element that defines the U-spline basis functions over that element as a linear combination of degree p Bernstein polynomials.
Quadrature
Since the U-spline basis functions are defined in terms of degree p Bernstein polynomials, they can be integrated exactly over each element using a n=(p+1)/2 quadrature rule. There is the potential for developing more efficient quadrature rules, but this an area of active research.
Hope this helps, and please let me know if you have any more questions.