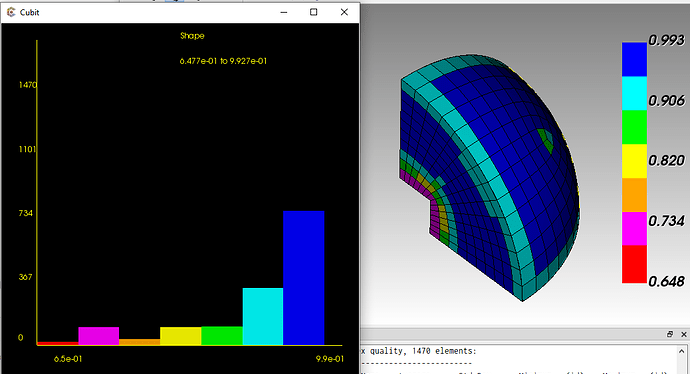
Cubit meshes a 2D circle and 3D sphere with the “cubed sphere” algorithm, but the inner “square” is stretched into a rectangle (maybe by a few percent). This is clearly seen in the manual under the circle meshing section. There seems to be no way to control this, and I cannot imagine why someone thought this was a good idea. Can this be reported as a “bug” to be fixed? I have a case were I really want as much symmetry in the cubed-sphere as possible. Of course the mesh could be build manually by other means, but I spent a lot of time debugging the FEM code only to discover that the issue was this meshing scheme.
Hi @jshaw,
Thank you for your comment.
Note that the shape of the interior is driven by the number of nodes on the exterior. In the example shown in the manual, there are 20 nodes on the exterior. This creates an odd number of nodes in a quadrant. That odd number of nodes in the quadrant will force a rectangular interior section (2x3 nodes). It sounds like the rectangular area does not exhibit the symmetry you are looking for.
You can create a “more” square interior by setting the number of nodes on the exterior to a number divisible by 8. In the example below, I set the number of nodes on the exterior curve to 24.
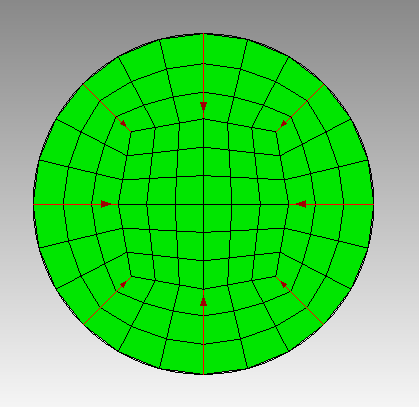
We are still fitting a square peg in a round hole so the distance from the exterior to the “square” is not equal. But all the vertical and horizontal distances are equal and the all the diagonal distances are equal.
The image above was created with the following script.
create surface circle radius 2
curve 1 interval 24
surface 1 scheme circle
mesh surf 1
Scheme circle will still have some inaccuracies due to the methods of placing the nodes based on a rectangular coordinate system. If you need an exact radial solution, you could look at the radialmesh option, 5.4 Meshing Schemes (coreform.com). This is a special case meshing algorithm for cases that required exact placement of nodes in a cylindrical coordinate system.
Do either of these answer your concerns?
Thanks,
Karl
Yes, this absolutely explains what is happening. Thank you! It did seem strange that someone would “chose” to make the box rectangular;) It may be necessary to build the 3D sphere from scratch to get the control I need. The real problem is a 3D sphere with a number of carefully controlled “shells” of various materials.
You might look at something like this to create the sphere quadrants. You wouldn’t normally think of this as a sweeping problem, but it works pretty well with some smoothing.
reset
create sphere radius 2 ypositive xpositive znegative
create brick x 1
subtract volume 2 from 1 keep
delete volume 1
compress
surface 7 8 9 int 5
mesh surf 7 8 9
vol 2 scheme sweep source surface 7 8 9 target surface 13
mesh vol 2

I can make the exterior surface look a little better by doing a smooth with the centroid area and then smoothing the volume as well.
surface 13 smooth scheme centroid area pull
smooth surface 13
volume 2 smooth scheme smart laplacian
smooth vol 2
This increases the overall number of well-shaped elements.
Karl