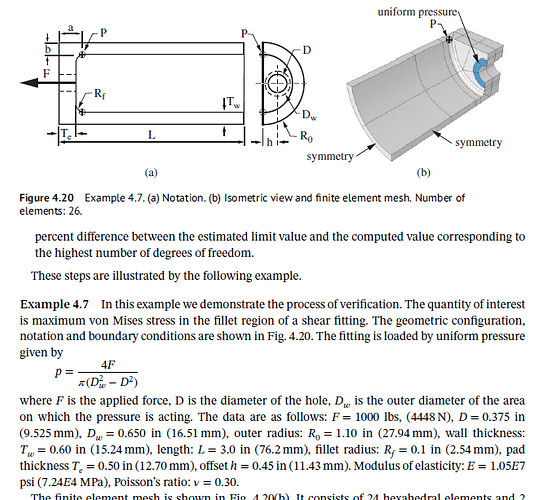
I listened to the webinar today. It occurred to me that the FEM with splines is exposed to the same predicament as the p-type FEM: the convergence needs to be determined from data that is not easy to extrapolate from. Here is a typical example from the textbook by Szabo, Babuska:
Notice the irregular curve for the p-version: so how do we estimate the limit value?
By the way, it isn’t at all clear how the 12.43 number was arrived at in the textbook.
Hi @PetrKryslUCSD, welcome to the forum!
Thanks for clarifying the question that I believe you asked during the webinar. Your question is a good one, perhaps the best way to answer it would be to provide a demonstration of the example alongside my response. I’m curious whether the example provided is from the new (2021) edition of Szabo and Babuska – I went to the library and checked out the first edition:

and couldn’t find the example. It appears that the limit solution they used is just the final value of the h-version data-series.
I’ll look to reply shortly with a response to your question!
Hi Greg,
Yes, the example is from the 2021 book.
I think the question of convergence is fundamental. I did not find
the arguments in the literature convincing. For instance, SolidWorks has the ability to
solve the problem with p-adaptivity (it used to have it, last time I checked was probably two to three years ago). I tried it, and the conversion graphs were typically irregular as shown above.
P
I have a suspicion that data is garbage. The thickness of the wall seems to be too large.
Yes - I noticed that as well. I’ve made some judgement calls on the dimensions to make it work.
I think the thickness should be only half of that, 0.3 in.
Dw seems to be also wrong.