Ellipsoid creation tolerance seems very low (sphere + scale); how to obtain higher geometric accuracy?

tloudon · December 17, 2025, 6:19pm

Coreform Cubit Version: Cubit 16.14
Platform: Windows

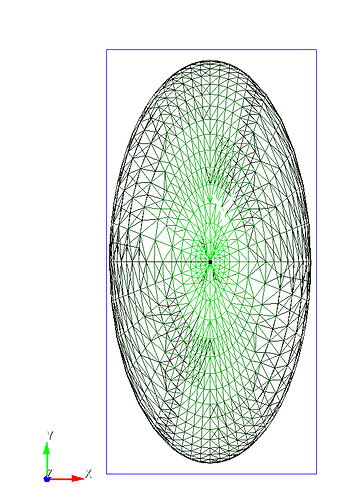
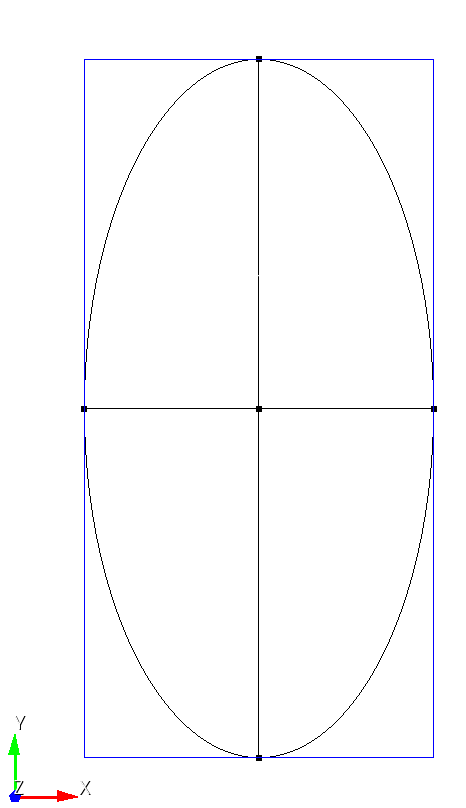
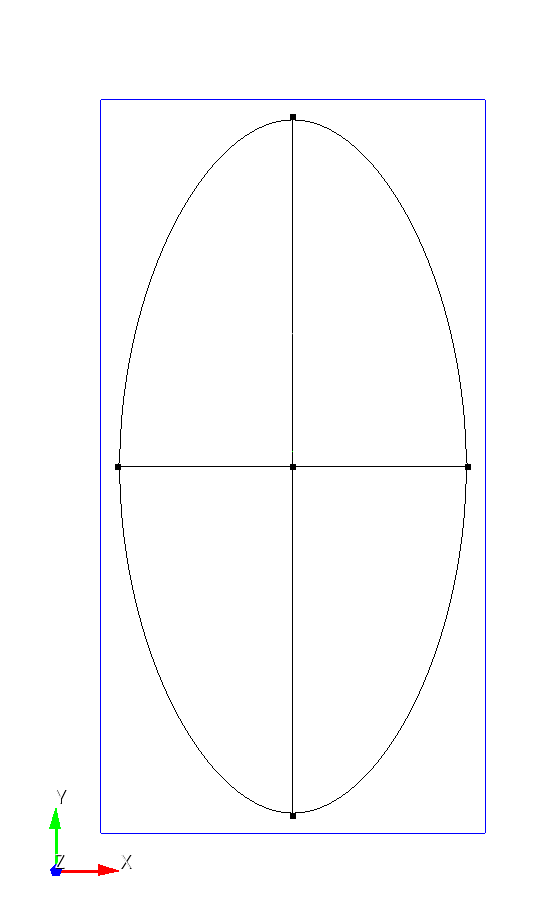
I am seeing unexpectedly large geometric errors when creating an ellipsoid by (1) creating a unit sphere and (2) scaling it anisotropically. The issue is especially pronounced for small ellipsoids, where the axis-aligned bounding box (AABB) lengths deviate substantially from the intended semi-axes.

# Import
import numpy as np
cubit.reset()

# Create ellipsoid (x/a)**2 + (y/b)**2 + (z/c)**2 = 1
a, b, c = 1., 2., 3.
cubit.cmd('sphere r 1')
vol_id = cubit.get_last_id('volume')
cubit.cmd(f'vol {vol_id} scale x {a} y {b} z {c}')

# Compute relative errors (using AABB extents)
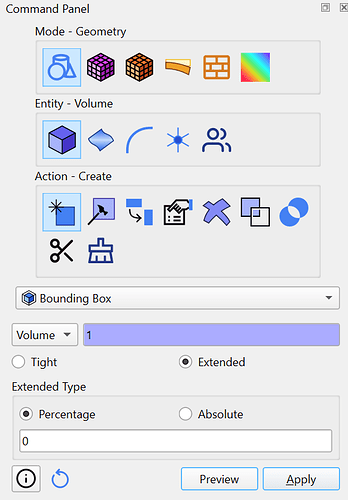
aabb = cubit.volume(vol_id).bounding_box()
x_length = aabb[3] - aabb[0]
y_length = aabb[4] - aabb[1]
z_length = aabb[5] - aabb[2]
print(f'Relative error in total x-axis length = {np.abs(x_length-2*a)/(2*a)}')
print(f'Relative error in total y-axis length = {np.abs(y_length-2*b)/(2*b)}')
print(f'Relative error in total z-axis length = {np.abs(z_length-2*c)/(2*c)}')

# Create smaller ellipsoid
a, b, c = 0.01, 0.02, 0.03
cubit.cmd('sphere r 1')
vol_id = cubit.get_last_id('volume')
cubit.cmd(f'vol {vol_id} scale x {a} y {b} z {c}')

# Compute relative errors
aabb = cubit.volume(vol_id).bounding_box()
x_length = aabb[3] - aabb[0]
y_length = aabb[4] - aabb[1]
z_length = aabb[5] - aabb[2]
print(f'Relative error in total x-axis length = {np.abs(x_length-2*a)/(2*a)}')
print(f'Relative error in total y-axis length = {np.abs(y_length-2*b)/(2*b)}')
print(f'Relative error in total z-axis length = {np.abs(z_length-2*c)/(2*c)}')

Output observed

For a,b,c = 1,2,3:

Relative error in total x-axis length ≈ 0.0404
Relative error in total y-axis length ≈ 0.0532
Relative error in total z-axis length ≈ 0.00033

For a,b,c = 0.01,0.02,0.03:

Relative error in total x-axis length ≈ 0.2590
Relative error in total y-axis length ≈ 0.7612
Relative error in total z-axis length ≈ 0.0333

Thanks in advance for any help.

gvernon · December 17, 2025, 8:18pm

Hi @tloudon - I believe you’ve discovered absolute tolerance in the ACIS CAD kernel that is at the heart of Coreform Cubit, and possibly a bug.

@kgmerkley - I don’t seem to get any differences whether I use set facet bbox on or set facet bbox off…

If I use the facet-rendering mode (graphics mode facet) and then preview the axis-aligned bounding box:

I don’t see any bad facets that would be responsible for the poor bounding box (blue) calculation:

Box center: x=0.013352, y=-0.000000, z=0.000000
Box dimensions: x=2.080759, y=4.212928, z=6.002000

It seems like, if we’re using set facet bbox on that we should be able to get a really good approximation to the bounding box.

Note that if I compute equivalent ellipse curves (via webcuts & copies) and compute the bounding box on the curves I get what I expect (or close to it):

Box center: x=0.000000, y=0.000000, z=0.000000
Box dimensions: x=2.002000, y=4.002000, z=6.002000

Note the error term in each of these dimensions appears to be absolute (0.002)

If we use the ellipsoid that is (effectively) scaled by 0.01 from the large ellipsoid the bounding box on the curves is less-good:

Box center: x=0.000000, y=0.000000, z=0.000000
Box dimensions: x=0.022000, y=0.042000, z=0.062000

Note the same absolute error between the large and small ellipsoids.

This has me thinking a few possible things:

Is set facet bbox [ON|off] broken? Is there a new command to use instead?
When using the ACIS kernel for the bbox calculation do we need to expose a tolerance value that the kernel uses to the user? Should this simply inherit the value of set geometry accuracy <value>?
If we’re using the facets for the bbox calculation, then this certainly seems to be a bug?

kgmerkley · December 19, 2025, 3:00pm

Right now, I’m leaning towards this being a bug. If I just create a ellipsoidal curve, the AABB is correct.

create vertex 1 0 0
create vertex 0 2 0
create vertex 0 0 0
create curve vertex 1 vertex 2 vertex 3 ellipse start angle 0 stop angle 360
draw bounding box Curve 1  extended percentage 0

**

**

If I take a different approach to creating an ellipsoid without the z component, I still get the correct bounding box.

reset
create vertex 1 0 0
create vertex 0 2 0
create vertex 0 0 0
create curve vertex 1 vertex 2 vertex 3 ellipse start angle -90 stop angle 90

create vertex 0 0 1
create curve arc center vertex 3 1 5 radius 1 normal 0 1 0 full
sweep curve 1  along curve 2  
delete curve all
delete vertex all
webcut body 1 plane zplane
stitch body all
compress
draw bounding box body 1  extended percentage 0

This lists the bounding box dimensions as exactly 2x4x2

If I scale that ellipsoid in the z direction, the bounding box dimensions vary from the exact dimensions.

If however, I start with the original problem, webcut the ellipsoid into 8 sections, and look at the vertex positions, the bounding box calculation is exactly 2x4x6 as desired to 8 digits.

reset
sphere radius 1
vol 1 scale 1 2 3
webcut vol all plane xplane
webcut vol all plane yplane
webcut vol all plane zplane
draw bounding box vertex all extended percent 0
set digits 12
list vertex all

Looking at the actual vertex locations at 12 digits shows variations on the order of e-17 or less.

Name	Id	     X-coord	        Y-coord              Z-coord
----------------------------------------------------------------------------------------------------------
Vertex 1	1	-6.12323399574e-17	1.49975978266e-32	 3
Vertex 2	2	-6.12323399574e-17	1.49975978266e-32	-3

The bounding box listed for all volumes using

draw bounding box volume all extended percentage 0

shows Box dimensions: x=2.002000, y=4.002000, z=6.002000

That seems to confirm that this is a bug in the bounding box calculation. There is not a bug in the scaling or the actual geometry. I will get this added into Sandia’s bug tracking system.