Coreform Cubit Version: 2025.8
Platform: Ubuntu (Docker; latest)
Toy Problem
I’m trying to better understand how the input element size in Cubit translates to the edge lengths of the quad elements for different 2D meshing schemes.
Let’s use the following example:
create surface circle radius 0.5 zplane
surface all size 0.05
I’d ideally like the edge lengths of the elements to be as uniform as possible, which is why I apply the following mesh smoothing after constructing the mesh:
surface all smooth scheme edge length
smooth surface all
There are three strategies I can think of that would give us a quad mesh with relatively uniform element sizes:
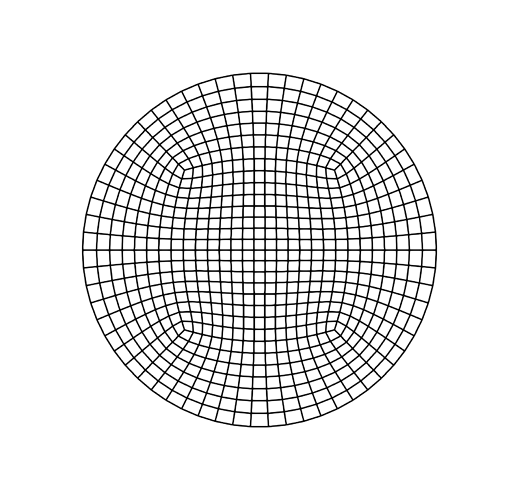
Option 1: Circle scheme
surface 1 scheme circle
mesh surface 1
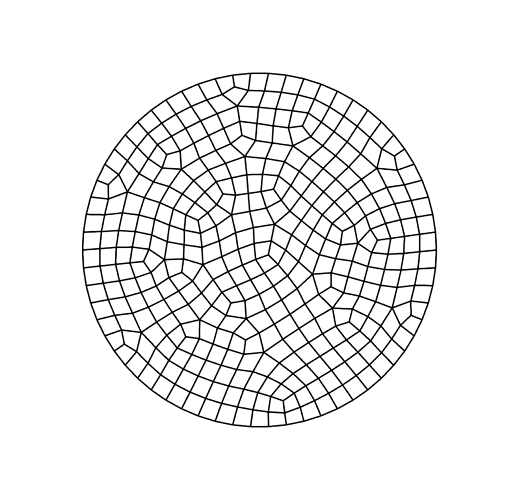
Option 2: Pave scheme
surface 1 scheme pave
mesh surface 1
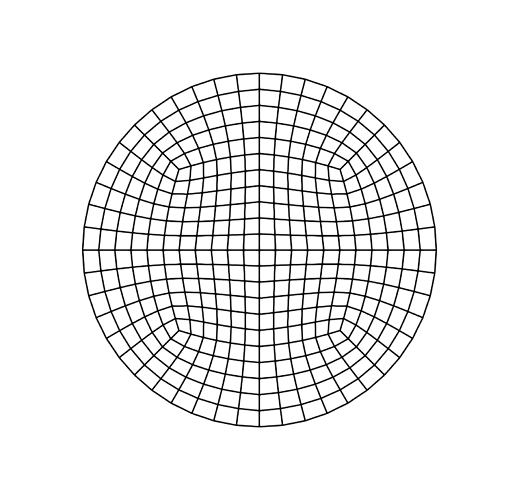
Option 3: Webcut the circle into quadrants and use Polyhedron scheme
webcut body all with plane xplane
webcut body all with plane yplane
merge curve all
surface all size 0.05
mesh surface all
Despite the element size being the same across all three schemes, the number of elements is dramatically different:
| Circle | Pave | Polyhedron | |
|---|---|---|---|
| Number of Elements | 674 | 384 | 354 |
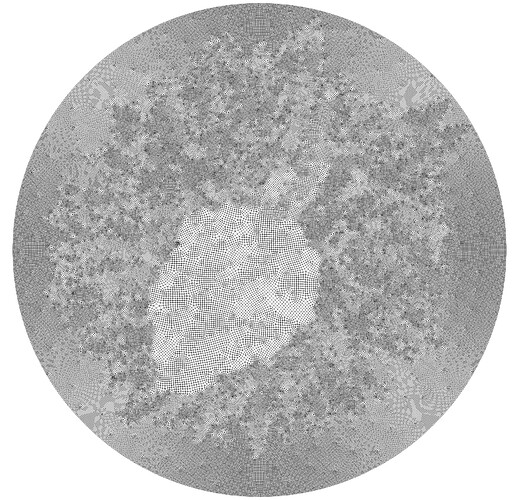
The elements in the polyhedral and circular meshes deviate quite a bit from the 0.05m input as the element size:
Most of the elements in the paved mesh are pretty close to the desired 0.05m though:
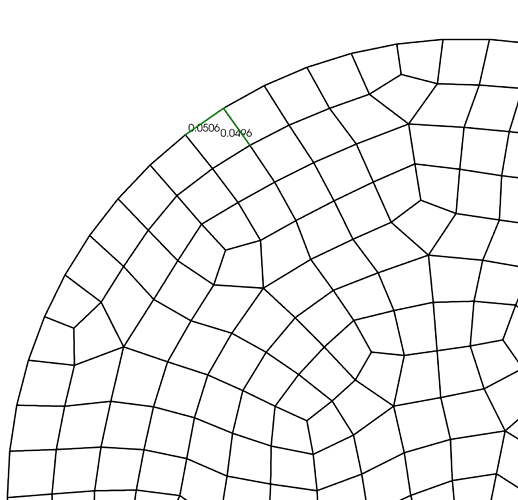
However, I’ve found that the paved meshes start to have inconsistent element sizes when the element size is very small relative to the geometry. Here’s what the mesh looks like with an element size of 0.0025m:
I realize I could webcut the domain and then pave each subdomain, but this feels a bit inefficient, given that the circle and polyhedron schemes would be able to mesh the domain much more quickly.
This brings me to a few questions:
- How does the input element size translate to the size of the elements for the
CircleandPolyhedronmeshing schemes? - Is there some additional setting I can use to achieve a more uniform element size in my mesh using these two schemes?
- Is there a way of mitigating the above discrepancy in element size when trying to pave surfaces where the element is very small relative to the size of the paving surface?