Welcome @Aakash!
I have a few questions about your question.
-
By “local mesh orientation” do you mean to use this for assigning a material orientation? Do you wish to assign a “local coordinate system” to mesh entities for this purpose?
-
For a general mesh / element, there is no single “local mesh orientation”. Am I correct in assuming that you are interested in capturing the local coordinate system at the center of the element? Essentially, evaluating the Jacobian at the parametric-center of the element?
For the second point, you’ll probably want to know the element local node ordering so you can build the basis / compute the Jacobian. To do this you can build a single element on a geometry that reflects the parametric shape of the element and use the Python interface to determine local node ordering. Example for hex:
cubit.cmd("reset")
cubit.cmd("brick x 2")
cubit.cmd("vol 1 interval 1")
cubit.cmd("mesh vol 1")
node_ids = cubit.get_entities("node")
node_loc = []
for n in node_ids:
node_loc.append(cubit.get_nodal_coordinates(n))
elem_conn = cubit.get_connectivity("hex", 1)
Printing node_loc shows:
[( 1, -1, 1),
( 1, 1, 1),
(-1, 1, 1),
(-1, -1, 1),
( 1, 1, -1),
( 1, -1, -1),
(-1, -1, -1),
(-1, 1, -1)]
and printing elem_conn shows:
(4, 7, 8, 3, 1, 6, 5, 2)
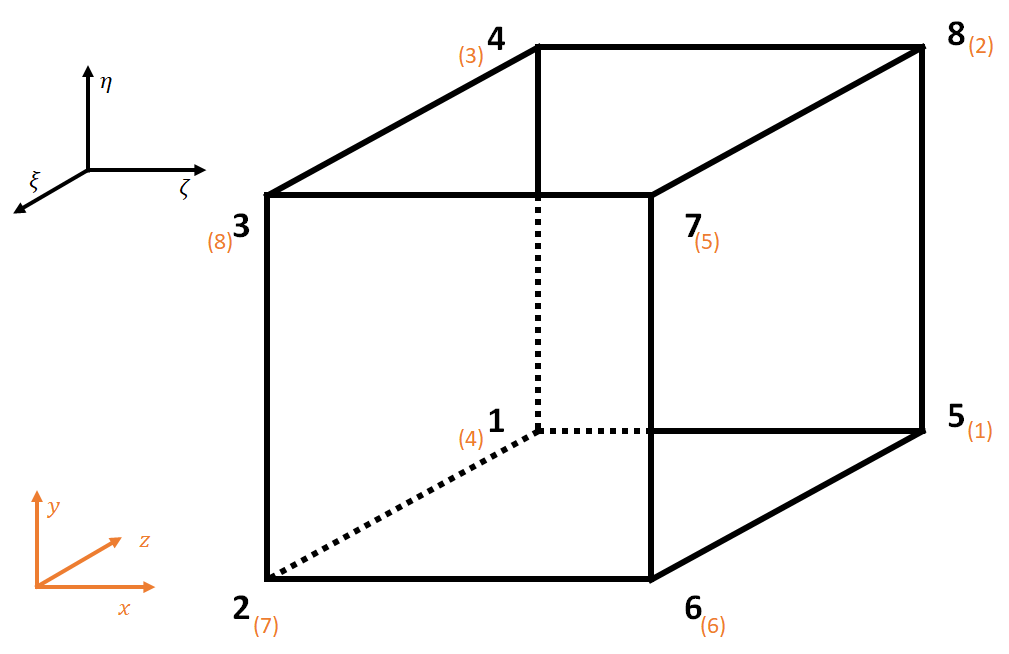
This can be visualized in the image below, where the black numbers & coordinates represent the local node-ordering and parametric coordinates, and the orange reflect the global coordinate system and global node-ids. Importantly, these are the local node orderings in Cubit – on export, these may have a different ordering depending on what code you’re exporting to (though the global node ids should remain consistent).
From there, you should be able to evaluate the coordinate system at each element’s center using Python to evaluate the Jacobian and apply it to the parametric coordinate system, which I think is what you want.